Minimum Phase Filters 最小相位滤波器简易
尊重原创,请勿转载!
作者:图林根の烤肠
理论上来说,所有的传递函数都可以写成如下的形式: 。其中 为我们需要的滤波器, 为全通滤波器(ap 为 All Pass缩写), 就是我们需要计算求出的最小相位滤波器。
为了得到最小的相位滤波器函数,具体的做法就是把 这个滤波器的零点(英语为Zero,德语 Nullstelle)放到单位圆(Unit Circle)里面。前面提到的零点通俗简单点说就是让 分数表达式分子等于零的解的位置。
下面来举个简单的例子:
上面的H1和H2就是两个滤波器函数。我们可以很容易的计算出 H1 的 零点 为 -1/2(让2+1/z=0,求出z为-0.5),同理 H2 的零点为 -2。具体形象些我们使用 matlab 画出 unit circle,并标出 零点和 极点:
|
|
结果如下所示:
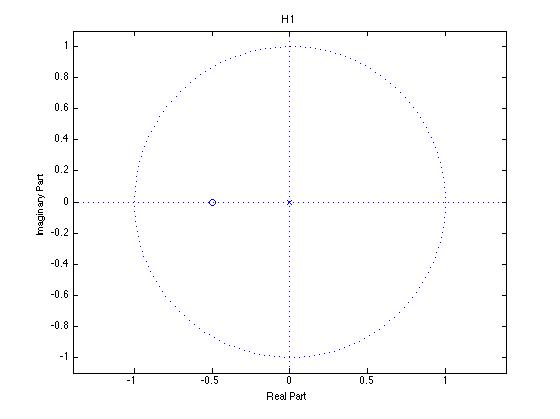
H1
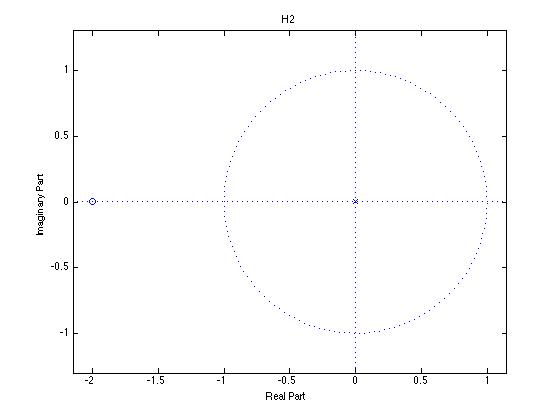
H2
从图中我们可以清楚的看到,零点(图中空心圆圈)的位置 H1(-0.5)位于圈内,H2(-2)位于圈外。为了获得最小的相位变化,我们需要把位于圈外的点镜像折叠到圈内,其做法是求Z模的倒数,这里的例子是,H2=-2 在圈外我们求其模的倒数便是 -0.5 (1/abs(2))。具体说是是否正确,我们来看频响,使用matlab 命令列出2个滤波器函数的频响图。
|
|
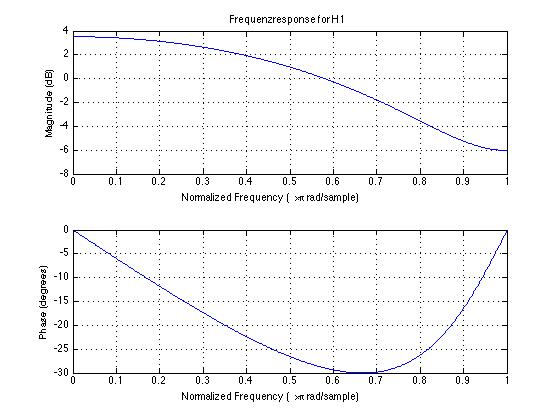
H1
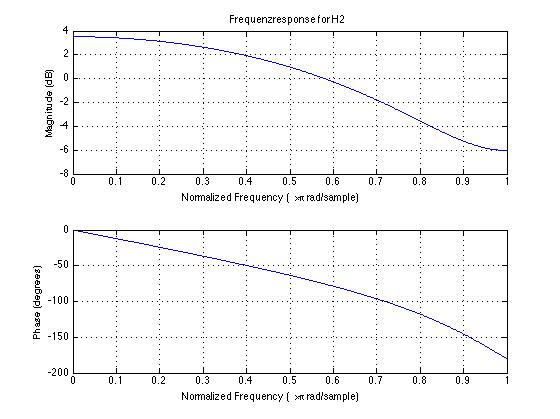
H2
我们只看 phase 这个纵轴,H1 的相位变化范围(0到-30度)明显要小于 H2 的相位变化范围(0到-200),所以说在保持频响(每一个图示的上图)相等的情况下,我们通过镜像变化零点得到了相位变化相对较小的滤波函数。
总结:
最小相位滤波器的主要算法就是通过镜像变化滤波函数的零点来得到的,然后再卷积一个全通滤波器就是我们最后想要的滤波器。我们可以通过保持频响不变的情况来获得相位变化相对较小的滤波函数,它有一个显著的点:滤波器的延迟最小,如果你打算设计一个延迟很低的滤波器,那么最小相位滤波器是首选。
参考资料:
- Minimum Phase Filters, Severin Ioan, Ilmenau University of Technology. P. O. Box 100565, D-98684 Ilmenau, Germany.