Vector Quantizer LBG 矢量量化简要实例算法

尊重原创，请勿转载!

作者：图林根の烤肠

最近忙于考试复习 ADSP (数字信号处理) 中，查看了一些资料，大多写的十分繁琐，一点都不生动形象，特此举个实例，方便理解，文章内容来源于课上的课件.

基本名词解释等相关资料可以从其它网站查询，这里只是实例举例： 输入的 Training Set 为：x = [3,2,4,5,7,8,8,9]。

我个人理解 Training Set 是一种替代 pdf 的方法，按照 N 维向量分割后的输入信号）。N 表示维数，如果 N = 2，表示的是二维空间，xy 二轴。

简要的计算方法：

1. 随机生成两个codebook vectors $y_{1}$ 与 $y_{2}$，比如说 $y_{1}$ = [1,2], $y_{2}$ = [5,6]，然后把 x 数值按照 N 维空间分类，这里 N = 2，所以分为[3,2], [4,5], [7,8], [8,9]即可。

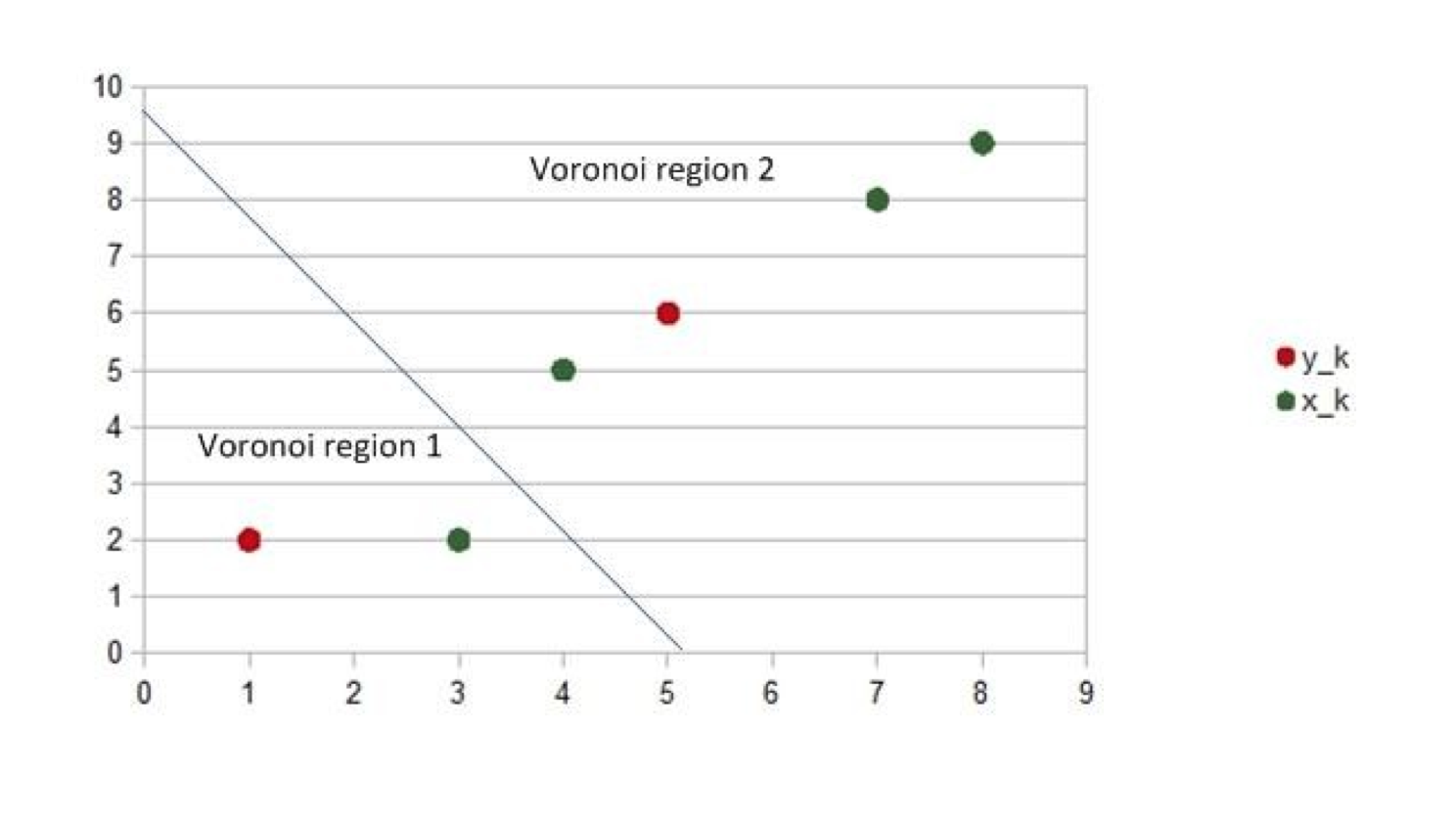
2. 求出 decision boundary $b_{k}$，其中 $b_{k}=(y_{1}+y_{2})/2$，我们可以求出 $b_{k} = [3,4]$。我们接下来就可以用一条直线来划分空间，注：此处的直线是垂直于连接 $y_{1}y_{2}$ 的直线，作用是 为了便于观察 才画出来的， 不影响计算机的其他运算。第三步的图片可以清晰说明。

3. 把所有的x点归类，划分到 $y_{1}$ 或者 $y_{2}$ 的空间里面，距离计算公式就是简单的两点间向量计算公式(参考下图)：对于点 $x_{1}$ = [3,2] 到 $y_{1}$ = [1,2] 的距离小于到 $y_{2}$ = [4,5] 的距离，所以可以把 $x_{1}$ 划分到图像左边的空间中。

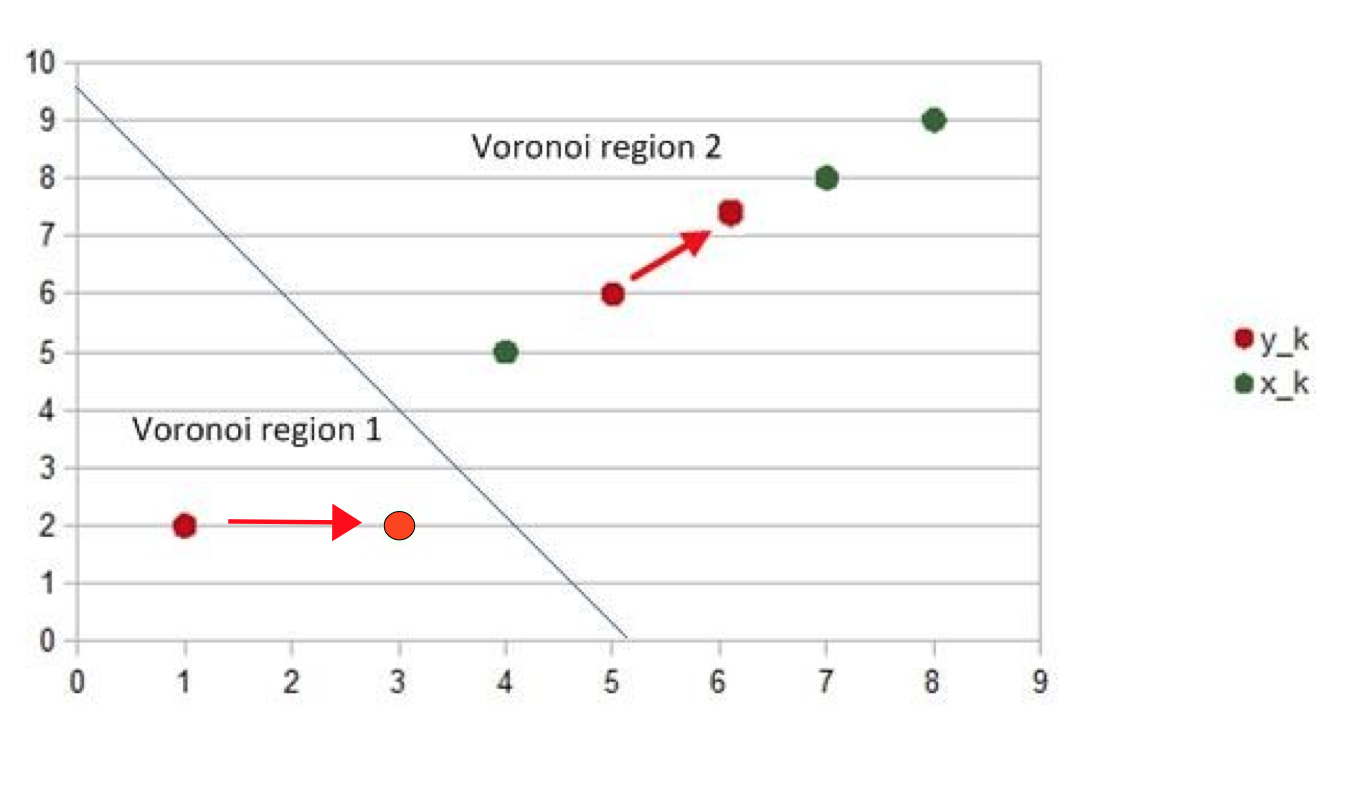
4. 计算新的 codewords $y_{k}$ 作为 Voronoi 空间的质心（centroid or conditional expectation ），其中的 $y_{k}$ 计算方法为

简要的说就是 Vornonoi 空间里所有的点的数值求和后再除以这个空间里面点的个数，此处的例子是：在 Voronoi region1 中只有一个点 $x_{1}$，所以新的 $y_{1}$ 为 $x_{1}$，也就是 [3,2]。再来看 Voronoi region 2 里面，$y_{2}$ 的计算方法为：

计算完后移动这两个 $y_{1}y_{2}$ 为新的质心重复第二步骤即可。

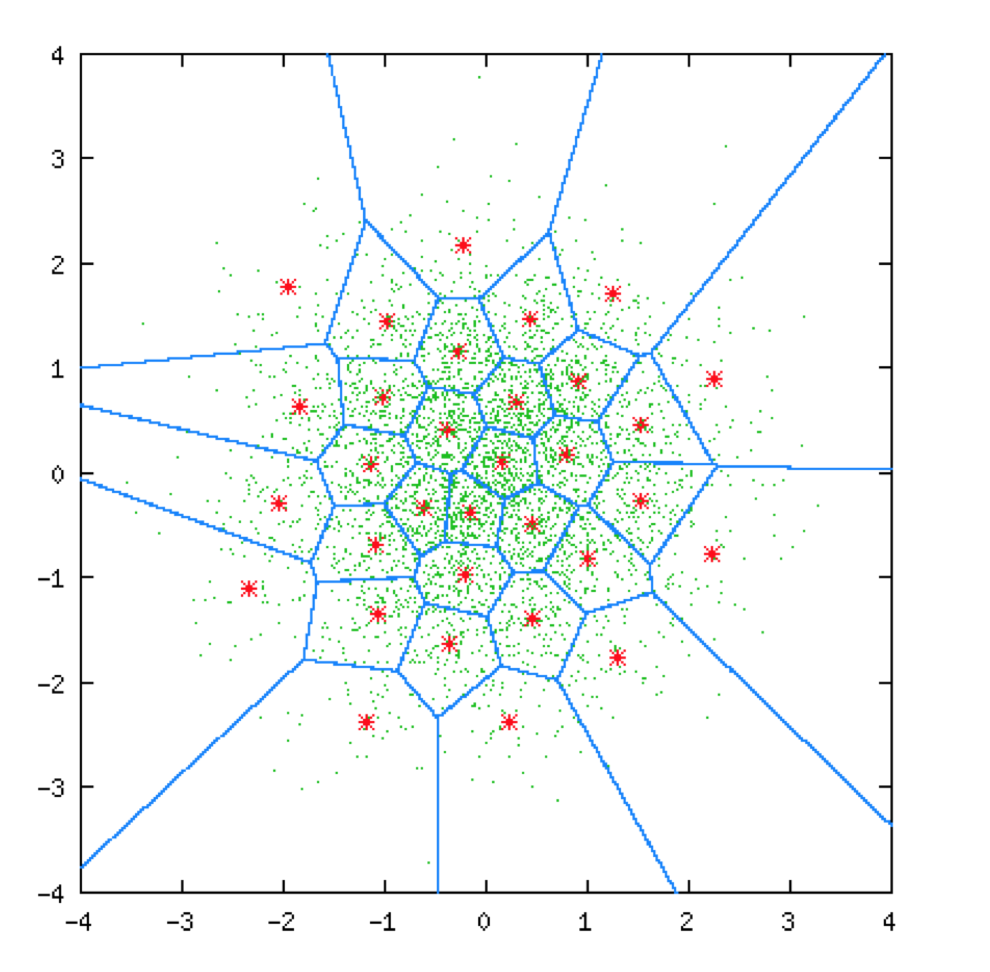
具体编程的例子就不写了，原理大概明白编起来也不是很困难的，最后通过这个算法的实际图例大概如下图所示，当然不是上面所举的那个例子。

最后推荐一个很好的 中文翻译相关博客

参考资料：

1. Digital Signal Processing 2/ Advanced Digital Signal Processing Lecture 5, Vector Quantizer, LBG Gerald Schuller, TU Ilmenau

2. http://www.data-compression.com/vq.html