Hermite Curve 以及 Bézier Curve 贝塞尔曲线的简要计算
Hermite Curve 以及 Bézier Curve 贝塞尔曲线的简要计算
尊重原创,请勿转载!
作者:图林根の烤肠
详细资料可以查询 wiki 的百科网站,以下内容为个人总结,难免出现错误,欢迎指正最后。
要了解Hermite以及Bézier,首先来简要了解这个三次参数曲线(Parametric cubic curves):
首先是一个空间三位曲线方程式如下:
这里面的 U 是scalar,B 是 basic function,而 G 就是 vector向量了,请注意这个线性方程可以转换为下图矩阵相乘的形式:
在了解了上面这个矩阵就可以开始正文了:
首先是 Hermite 曲线,它是由一些参数决定:
- 2个首位端点 P1,P4 及其各自的斜率参数 R1 与 R4
- Hermite 几何矢量(geometry vector)$G_{H}$
- Hermite 矩阵为:
Hermite 曲线最后的表述方式如前面介绍的三次参数曲线为: $Q(u) = U \cdot M_{h} \cdot G_{H}$。这里不仅有人要问,这 Hermite 矩阵为什么是这个样子,其中的推导过程在这偷个懒,直接拽张图片过来
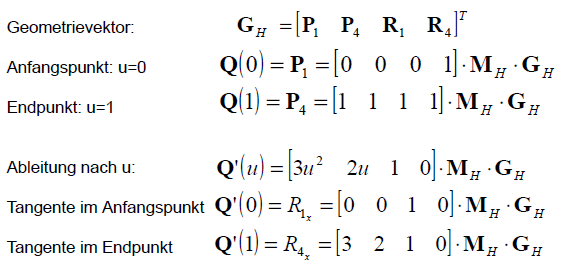
Q(0) 与 Q(1) 分别为 u=0 与 u=1 用特殊法。带入上面的三次曲线方程的结果,然后对其方程式求导,带入u=0与u=1,分别求出 Q(0) 与 Q(1) 的斜率。因为 Q(u) = [P1:P4:R1:P4](这是一个4行一列的矩阵),然后会得出一个等式:
又因为 $G_{H}$ 也等于[P1;P4;R1;P4], 所以方程两边可以消去[P1;P4;R1;P4]得到等式。
再求逆矩阵便可得到 Hermite 矩阵:
按照同样的方法,我们可以接下来获得贝塞尔曲线 Bézier Curve。下面这张图清晰直观的了解到 Bézier Curve 是一个三位空间曲线通过转换投影到2D平面的曲线。
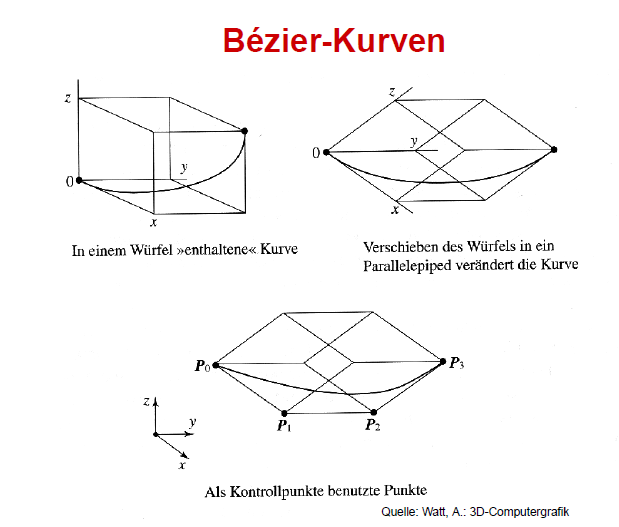
图片来源:Watt,A: 3D-Computergrafik
同上面介绍的 Hermite曲线计算一样,Bézier curve 同理表述为
或者以矩阵的形式表示:
其中 $P_{i}$ 为行向量 (row-vector),里面的推导过程就不介绍了,详情可以查询 维基百科 的网页介绍。 另外推荐一篇介绍 Hermite 曲线的 OpenGL 博客,非常值得一看。
参考资料:
3D-Repräsentation,Vorlesung Computeranimation WS 2009 © Nowak, Weigel, Kirchner, Schuller