G.711 a-law 及 u-law 简要算法过程
G.711 a-law 及 u-law 简要算法过程
尊重原创,请勿转载!
最近课上在讲 a-law 以及 $\mu$-law 的压缩算法,查了下 wiki,英文版的资料算是比较全的了,国内的那xx百科相比之下简直跟没有一样。
其中 a-law 和 $\mu$-lau 的公式分别如下:
$\mu$-lau 公式如下:
$\mu$-law 给出 $\mu$ 值为255,a-law 中的A赋值为87,6
由于课上老师只是介绍了 $\mu$-law,在此简要说明一下算法。 公式中的 x 是输入信号取值为 0到1,需要把 x信号归一化,此处为除以 A(最大波峰值),y 为输出信号,具体算法可根据应为 wiki 给出的公式如上面所示,其中sgn(x)表示输入信号的符号(正值为1,负值为-1),matlab 可用sign函数代替,然后进行采样量化,比如8bit线性采样,最后通过下图逆运算就可以得到关于 x 的函数,从而算出通过 $\mu$-law 编码的文件。
至于有人不禁要问,为什么这么折腾来回算一下,其实是因为,此算法同样适用于非均匀分布函数,一般的线性采样只能用于均匀分布信号,并且 SNR(信噪比) 不会有太大的变化。
参考资料:
- Digital Signal Processing 2/Advanced Digital Signal Processing Lecture 3. Gerald Schuller, TU Ilmenau
- http://www.dspguide.com/ch22/5.htm
补充说明
最近复习看了篇文章,明白了一些,稍微补充一点知识:
一般来说语音信号是符合拉普拉斯分布的,当我们使用线性量化的时候则会造成一些不必要的量化等级的浪费(这里还得请高人解答,不知道为什么),于是我们就把信号先进行放大,使其的pdf分布发生改变,使pdf变得更加的均匀,然后再进行量化反转,从而得到最终的信号。如下图所示:
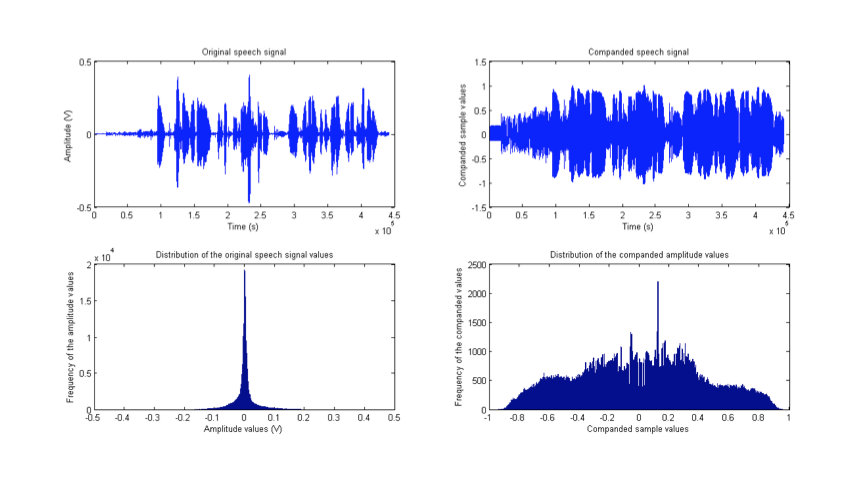
这样做的好处有两点:
- 提高的信噪比snr,如下图所示
- 降低了设备的需求,因为只是进行的一步简单的公式计算
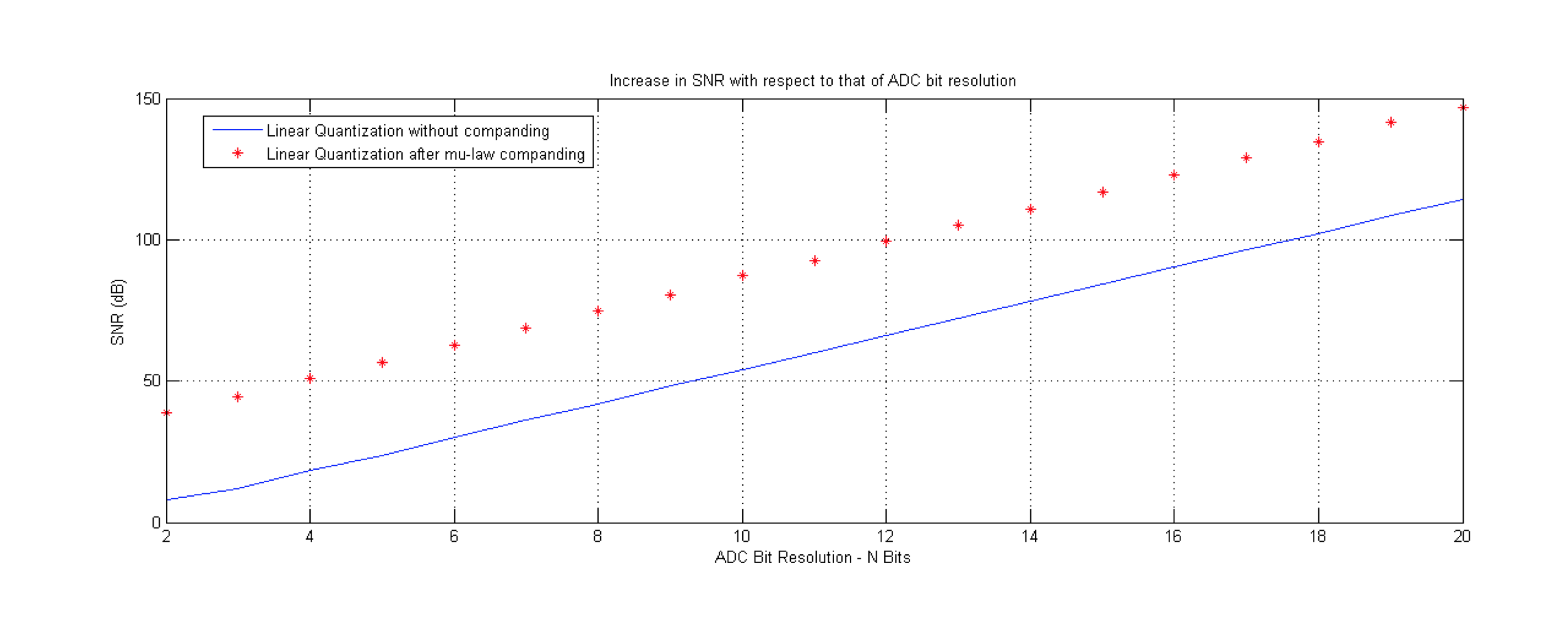
蓝色表示的是直接量化后得到的信噪比snr,红点为通过companding(信号扩展压缩)后然后得到的snr,明显可知要好于未经过扩展的原信号。但是a-lau和u-lau却不适合pdf变化非常剧烈的信号,这时候则需要其它更加优秀的算法,比如说Lloyds-Max和LBG算法。
参考资料:
- Non-uniform Quantization: Companding , μ-Law and A-Law ;
- Aravindan Joseph Benjamin. Digital Signal Processing Research Laboratory Ilmenau University of Technology. P. O. Box 100565, D-98684 Ilmenau, Germany. Email: aravindan-joseph.benjamin(at)tu-ilmenau.de